In the recent years, there has been an increasing interest in simulating financial systems using multi-agent models and Cellular Automata (CA). There is a strong feeling that financial markets are typical complex systems in which the global dynamical properties mainly depend on the evolution of a large number of non-linear interacting agents. An extreme view of this is to consider that much of the randomness of financial markets is the consequence of their dynamics and has little to do with the nature or value what is being trade. This is in contrast with classical models that assume that investors are rational and consider the price a random walk. In his book "A New Kind of Science", Stephen Wolfram has proposed a very simple and idealized model of a stock market. It is a one-dimensional CA where each cell corresponds to an entity that either buys or sells on each step. The behavior of a given cell is determined by the one of its two neighbors at the preceding step (see diagrams (C) S. Wolfram). The application on this rule results in a sort of random behavior that look likes those seen on stock markets curves.
This is true but the problem is that this model is so simple, not to say trivial, that we can use it to model almost everything. Well, I am probably too severe here, but we need a more realistic CA model to work on financial markets.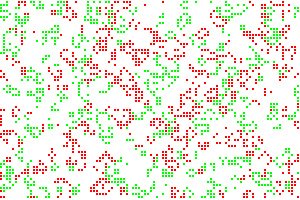 
I have tried to use a two-dimensional CA with three states: sell, keep or buy, and a more realistic transition rule. However, at this time, results are not very convincing from my point of view. The colored picture is a small part of a bigger image showing a typical run. One important feature of this model is the deterministic nature of its transition rule that contrast with most other studied stock market CA models. So, I hope to find something interesting the near future.
2 comments:
Quite interesting post. I didn't get how the 1D CA series is translated into a price series... I guess each price is previous price plus number of black cells minus number of white cells. Am I right?
As you said, 1D is too simple. Though less graphic, probably 2D is also too simple. I would say a higher dimensional, more compact world would be more realistic.
I strongly disagree with your conclusions about how Wolfram's model can be improved. The whole point of the concepts in "A New Kind of Science" is that a very complex model will be only slightly - if at all - superior to an extremely simple model. But principle discussions aside I am wondering what kind of input data you are using for your model. The major problem - as stated by Wolfram - is that in real markets you do not know what other entities are doing at a certain point in time and this information is the basis of the model. I have considered several possibilities to approximate that kind of information but they do not appear satisfactory to me... very curious about your approach!
Post a Comment